Poolcoördinaten

Poolcoördinaten $(r, θ)$ maken in de wiskunde deel uit van een tweedimensionaal coördinatenstelsel, waarbij de plaats van een punt wordt vastgelegd ten opzichte van een vast punt $O$ , de pool, en een halve lijn door dit punt, de poolas. Het is dus een stelsel met als argumenten de afstand tot het poolpunt en de hoek tot de poolas.

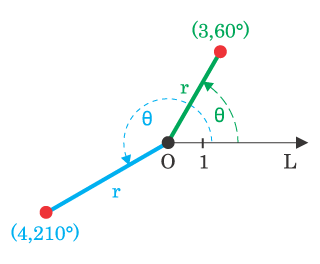
De coördinaat $r$ , de straal, van een punt $P$ is de afstand $O P$ tot de pool en de tweede coördinaat $θ$ , het argument, is de georiënteerde hoek tussen de halve lijn van $O$ door $P$ en de poolas. Uit deze definitie blijkt dat het argument van een punt $P$ niet eenduidig bepaald is. Met het argument $θ$ in radialen, zijn ook alle hoeken $θ + 2 k π$ voor gehele $k$ argument van $P$ . Het bereik van $θ$ wordt daarom in het algemeen wel beperkt tot bijvoorbeeld $0 \leq θ < 2 π$ of $- π < θ \leq π$ . Voor de pool zelf is $r = 0$ en $θ$ onbepaald.

Poolcoördinaten en cartesische coördinaten

Het verband tussen de cartesische coördinaten $(x, y)$ en de poolcoördinaten $(r, θ)$ wordt gegeven door:

x = r \cos (θ)

y = r \sin (θ)

Omgekeerd geldt:

r = \sqrt{x^{2} + y^{2}}

θ = \arctan (\frac{y}{x})

Hierin is gebruikgemaakt van de uitgebreidere definitie van de arctangens:

\arctan (y, x) = - i \log (\frac{x + i y}{\sqrt{x^{2} + y^{2}}})

Met behulp van de gewone arctangens kan men de hoek $θ$ als volgt in het interval $(- π, π]$ bepalen:

θ = {\begin{matrix} \arctan (\frac{y}{x}) & voor x > 0 \\ \arctan (\frac{y}{x}) + π & voor x < 0, y \geq 0 \\ \arctan (\frac{y}{x}) - π & voor x < 0, y < 0 \\ + \frac{1}{2} π & voor x = 0, y > 0 \\ - \frac{1}{2} π & voor x = 0, y < 0 \end{matrix}

Voorbeeld

Nemen we als voorbeeld het punt in het platte vlak met cartesische coördinaten:

x = 3, y = 2

$(3, 2)$ heeft als poolcoördinaten:

r = \sqrt{3^{2} + 2^{2}} = \sqrt{13}

en

θ = \arctan (\frac{2}{3})

.

Coördinatentransformatie

De jacobi-matrix van de bovengenoemde overgang van cartesische naar poolcoördinaten wordt bepaald door:

d x = \cos (θ) d r - r \sin (θ) d θ

d y = \sin (θ) d r + r \cos (θ) d θ

In matrixnotatie wordt dit:

[\begin{matrix} d x \\ d y \end{matrix}] = [\begin{matrix} \cos (θ) & - r \sin (θ) \\ \sin (θ) & r \cos (θ) \end{matrix}] [\begin{matrix} d r \\ d θ \end{matrix}]

Voor de booglengte geldt

(d s)^{2} = (d r)^{2} + r^{2} (d θ)^{2}

Als een integraal in het $x y$ -vlak naar poolcoördinaten $r$ en $θ$ moet worden omgezet, wordt het verband tussen de oppervlakte-elementjes $d x d y$ en $d r d θ$ gegeven door

d x d y = r d r d θ = | \frac{\partial (x, y)}{\partial (r, θ)} | d r d θ

De determinant in deze vergelijking is de jacobi-matrix van de coördinatentransformatie:

| \frac{\partial (x, y)}{\partial (r, θ)} | = | \begin{matrix} \cos (θ) & - r \sin (θ) \\ \sin (θ) & r \cos (θ) \end{matrix} | = r

Vectorveld

Het is gebruikelijk een vectorveld

F (x, y) = (F_{x} (x, y), F_{y} (x, y))

in poolcoördinaten te ontbinden in een component $F_{r}$ langs de poolstraal en een component $F_{θ}$ loodrecht daarop in de richting van de hoek $θ$ . Voor deze componenten geldt:

F_{r} = F_{x} \cos (θ) + F_{y} \sin (θ)

F_{θ} = - F_{x} \sin (θ) + F_{y} \cos (θ)

Omgekeerd:

F_{x} = F_{r} \cos (θ) - F_{θ} \sin (θ)

F_{y} = F_{r} \sin (θ) + F_{θ} \cos (θ)

Complexe getallen

Poolcoördinaten kunnen ook worden gebruikt om complexe getallen weer te geven in het complexe vlak. Het complexe getal $z$ kan cartesisch worden weergeven als $z = x + i y$ waarin $x$ het reële deel is en $y$ het imaginaire deel. Met poolcoördinaten kan $z$ als $z = r e^{i θ}$ worden geschreven, waarin $r$ de absolute waarde van $z$ is en $θ$ het argument in radialen.

Het punt $(- 1, 0)$ gegeven in cartesische coördinaten komt met $(r, θ)$ in poolcoördinaten overeen. Daaruit volgt de identiteit van Euler:

e^{i π} + 1 = 0

Poolvergelijking

Een poolvergelijking is een vergelijking tussen de variabelen $r$ en $θ$ . Dit verband wordt meestal in de vorm $r = f (θ)$ geschreven of impliciet als $F (r, θ) = 0$ . Daarin wordt de hoek $θ$ altijd in radialen gegeven. Bij een gekozen stelsel poolcoördinaten vormen de oplossingen van een dergelijke vergelijking de grafiek van de poolvergelijking. Dezelfde grafiek kan bij verschillende poolvergelijkingen horen. De hoek $θ$ mag in de vergelijking $r = f (θ)$ in principe alle reële getallen doorlopen.

Onder de richting van een kromme $K$ in een punt $𝛱 = (r_{𝛱}, θ_{𝛱})$ verschillend van de pool wordt de richting van de raaklijn in $𝛱$ aan $K$ verstaan, georiënteerd in de zin van toenemende waarden van $θ .$ De richting kan uit de hoek $α$ worden bepaald tussen de raaklijn in $𝛱$ en de voerstraal $O 𝛱$ . Voor deze hoek geldt:

\cot α = \frac{d}{d θ} \ln (r) = \frac{1}{r} \frac{d r}{d θ}

Voor bijvoorbeeld de logaritmische spiraal is $α$ constant.

Alternatieve definitie van poolcoördinaten

$(r, θ)$ en $(r^{'}, θ^{'}) = (- r, θ + π)$ zijn twee paren poolcoördinaten van hetzelfde punt $P$

Het kan in sommige gevallen nuttig dat de voerstraal $r$ ook negatieve waarden kan aannemen. Om dit mogelijk te maken kan men de definitie van het poolcoördinatenstelsel iets veranderen.

Het coördinatenstelsel bestaat dan uit een vast punt $O$ , de pool en een as door dit punt, de poolas. Om de poolcoördinaten van een punt $P$ vast te leggen kiest men een as $u$ door $O P$ . De abscis $r$ van het punt $P$ op die as, met oorsprong $O$ , is de eerste coördinaat $r$ van $P$ . Deze waarde kan negatief zijn. Als tweede coördinaat kiest men een van de mogelijke waarden van de georiënteerde hoek $θ$ tussen de as $u$ en de poolas. Ook hier kan het punt $P$ meer paren poolcoördinaten hebben.

Als $r$ een differentieerbare functie van $θ$ is die door nul gaat voor $θ = θ_{0}$ , raakt de door $r$ beschreven kromme daar aan de lijn $θ = θ_{0}$ . Bij toelaten van een negatieve $r$ gaat voor die $θ = θ_{0}$ de kromme door $O$ , anders eindigt de kromme bij $O$ . Als de functie weer door nul gaat bij $θ = θ_{1}$ , met $r < 0$ voor $θ_{0} < θ < θ_{1}$ , dan is de kromme bij toelaten van een negatieve $r$ een gladde zichzelf in $O$ snijdende kromme. Wordt een negatieve $r$ niet toegelaten, dan vervalt het deel $θ_{0} < θ < θ_{1}$ en heeft de kromme in $O$ een knik.

In natuurkundige formules betekent $r$ vaak de norm van de plaatsvector $𝐫$ . Dat is dan een niet-negatieve grootheid, die dus van de $r$ moet worden onderscheiden, die negatief kan zijn. Een grootheid kan alleen in $r$ en $θ$ worden geschreven als dat bij negatieve $r$ correct blijft. Zo is de grootte van de middelpuntzoekende versnelling dan niet $r ω^{2}$ , maar $| r | ω^{2}$ . Anders gezegd: de versnelling is dan in de richting van afnemende $| r |$ en niet noodzakelijk in de richting van afnemende $r$ . Rekening moeten houden met een negatieve $r$ wordt zo al gauw onnodig ingewikkeld.

Voorbeelden

Lijn

De vergelijking in poolcoördinaten van een halve lijn, of als $r$ ook negatief kan zijn een lijn, door de pool is van de vorm $θ = c$ , een constante. De vergelijking van een lijn die niet door de pool gaat, is

r = \frac{b}{\cos (θ - θ_{0})}

waarin $b$ de afstand van de lijn tot de oorsprong is en $θ_{0}$ de richting loodrecht op de lijn. Een vergelijking van de lijn door de punten $A = (r_{1}, θ_{1})$ en $B = (r_{2}, θ_{2})$ is

r_{1} \cdot r_{2} \sin (θ_{2} - θ_{1}) + r_{2} \cdot r \sin (θ - θ_{2}) + r \cdot r_{1} \sin (θ_{1} - θ) = 0

$r$ mag hierin ook negatief zijn.

Cirkel

De poolvergelijking van een cirkel met middelpunt in de pool en straal $R$ is $r = R$ . Een vergelijking van een cirkel met middelpunt $(r_{1}, θ_{1})$ en straal $R$ is

r^{2} - 2 r r_{1} \cos (θ - θ_{1}) + r_{1}^{2} = R^{2}

De grafiek van

r = 2 R \cos (θ)

is een cirkel met middelpunt $(R, 0)$ door de pool $O$ .

$r$ mag ook hier negatief zijn.

Kegelsnede

Een poolvergelijking van een kegelsnede met excentriciteit $ε,$ een brandpunt in de pool en de corresponderende richtlijn loodrecht op de poolas is van de vorm

r = \frac{p}{1 - ε \cos θ}

Daarin is $p$ nog een parameter.

Als $r$ niet negatief mag worden is de grafiek van de vergelijking in het geval van een hyperbool maar één tak en moet $p$ in de overige gevallen positief zijn. Als een negatieve waarde voor $r$ niet wordt toegelaten, zijn $r = 5 / (1 + 3 \cos θ)$ en $r = 5 / (- 1 + 3 \cos θ)$ bijvoorbeeld de vergelijkingen van de takken van een hyperbool, maar anders elk de vergelijking van de hele hyperbool.

De poolvergelijking van een ellips met de pool in het middelpunt en de poolas op de lange as, en met lange as $2 a$ en korte as $2 b$ is:

r = \frac{a b}{\sqrt{(b \cos θ)^{2} + (a \sin θ)^{2}}}

Rotatie en poolvergelijking

Kromme $r = \sin (2 θ)$ ; in de rechter figuur is $r$ niet negatief

Draait men een kromme $K$ met poolvergelijking $F (r, θ) = 0$ om de pool over een hoek $α$ , dan heeft de geroteerde kromme een vergelijking $F (r, θ - α) = 0$

Voorbeeld

De kromme $K$ is gegeven door de poolvergelijking $r = \sin 2 θ$ . Wordt de kromme over $π$ radialen om de pool geroteerd, dan is de vergelijking van de gedraaide kromme $K^{'}$ :

r = \sin 2 (θ - π) = \sin (2 θ - 2 π) = \sin 2 θ

De krommen $K$ en $K^{'}$ voldoen aan dezelfde vergelijking, ze vallen samen.

Meer dimensies

Poolcoördinaten zijn ook geschikt voor gebruik in meer dan twee dimensies. Er zijn verschillende generalisaties mogelijk. In het algemeen geldt dat een punt in de $n$ -dimensionale ruimte geïdentificeerd wordt door $(r, θ_{1}, \dots, θ_{n - 1})$ , een voerstraal en $n - 1$ welgedefinieerde hoeken.

Bol- en cilindercoördinaten

Het poolcoördinatenstelsel voor een 3D-ruimte wordt het bolcoördinatenstelsel $(r, θ, φ)$ genoemd en wordt met behulp van een extra hoek $φ$ gegeven. Het wordt veel in de exacte wetenschappen gebruikt om er de punten op of in een bol of een bolvormig lichaam mee te beschrijven. Voor cilinders wordt van cilindercoördinaten $(r, θ, z)$ gebruik gemaakt, die ook van de 2D-poolcoördinaten zijn afgeleid.

Bolcoördinaten $(r, θ, φ)$
Cilindercoördinaten $(r, θ, z)$

Websites

Poolcoördinaten. gearchiveerd op 9 september 2013
MathWorld. Polar Coordinates.
Polar Graphs. applicatie waar JRE voor nodig is
Wikibooks. Poolcoördinaten. in het Wikibook Klassieke Mechanica/Kinematica

Poolcoördinaten

Inhoud