Vlechtgroep

In de groepentheorie, een deelgebied van de wiskunde, is de vlechtgroep op n strengen, aangeduid met $B_n$, een groep die een intuïtieve meetkundige weergave heeft, en die in zekere zin het concept van een symmetrische groep $S_n$ generaliseert. Als het natuurlijke getal $n$ groter is dan 1, is $B_n$ een oneindige groep. Vlechtgroepen hebben toepassingen in de knopentheorie, aangezien elke knoop kan worden weergegeven door de afsluiting van bepaalde vlechten.

Geschiedenis

Vlechtgroepen werden in 1925 door Emil Artin geïntroduceerd, hoewel Wilhelm Magnus er in 1974 op heeft gewezen dat vlechtgroepen impliciet reeds in 1891 in het werk van Adolf Hurwitz over monodromie voorkwamen. Magnus beweert in essentie dat Hurwitz de interpretatie van een vlechtgroep als de fundamentaalgroep van een configuratieruimte gaf, een interpretatie waar daarna lang niets mee is gedaan, totdat deze interpretatie in 1962 met de ontwikkeling van de vlechttheorie door Ralph Fox en Lee Neuwirth opnieuw werd gebruikt.

Intuïtieve beschrijving

Deze introductie gaat uit van $n=4$, maar vlechtgroepen met andere waarden van $n$ zijn op dezelfde samengesteld. Beschouw twee verzamelingen van vier voorwerpen die op een tafel liggen, waar de voorwerpen in elk van de verzamelingen in een verticale lijn worden gerangschikt, zodanig dat de ene verzameling zich naast de andere bevindt. Die voorwerpen zijn in de onderstaande illustratie de zwarte stippen. Met vier strengen wordt nu elk item in de linker verzameling verbonden met een item in de rechter verzameling, zodanig dat er een een-op-een correspondentie ontstaat. Een dergelijke verbinding wordt een vlecht genoemd. Vaak zullen bepaalde strengen over elkaar heen of onder elkaar door lopen en dit is cruciaal: de volgende twee verbindingen zijn verschillende vlechten.

De vlecht ${\sigma }_1^{-1}$

verschilt van de vlecht ${\sigma }_1$

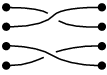
Aan de andere kant worden twee van zulke verbindingen, die men er hetzelfde uit kan laten zien door "aan de strengen te trekken", als dezelfde vlecht beschouwd:

De vlecht ${\sigma }_1^{-1}$

is hetzelfde als de vlecht

Van alle strengen vereist men dat deze zich van links naar rechts bewegen; vlechten met knopen erin, zoals de onderstaande, worden niet als vlechten beschouwd:

Deze configuratie

is geen vlecht

Twee willekeurige vlechten kunnen worden samengesteld door de eerste naast de tweede te tekenen, de vier items in het midden met elkaar te laten samenvallen en de corresponderende strengen te verbinden:

samengesteld met

levert op

Een ander voorbeeld:

samengesteld met

levert op

De samenstelling van vlechten $\sigma$ en $\tau$ wordt geschreven als $\sigma \tau$.

De verzameling van alle vlechten met vier strengen wordt aangeduid met $B_4$. De bovenstaande samenstelling van vlechten is een groepsbewerking. Het neutrale element is de vlecht, die uit vier evenwijdige horizontale strengen bestaat, en het inverse element van een vlecht maakt de groepsbewerking van de eerste vlecht ongedaan, dit ongeacht wat de eerste vlecht heeft uitgevoerd. De eerste twee voorbeeldvlechten in het voorbeeld hierboven zijn inversen van elkaar.

Generatoren en relaties

Beschouw de onderstaande drie vlechten:

${\sigma }_1$	${\sigma }_2$	${\sigma }_3$

Elke vlecht in $B_4$ kan worden geschreven als een samenstelling van een aantal van deze vlechten en hun inversen. Met andere woorden, deze drie vlechten brengen de groep $S_4$ voort. Om dit in te zien wordt een willekeurige vlecht van links naar rechts gescand. Als men een kruising van de strengen $i$ en $i+1$, vanaf de top op het punt van de kruising geteld, tegenkomt, wordt ${\sigma }_i$ of ${\sigma }_i^{-1}$ genoteerd, afhankelijk van het feit of streng $i$ onder of over streng $i+1$ heen beweegt. Bij het bereiken van de rechterkant is de vlecht geschreven als een product van de $\sigma$'s en hun inversen.

Het is duidelijk dat:

${\sigma }_1{\sigma }_3={\sigma }_3{\sigma }_1$

De twee volgende relaties zijn echter minder duidelijk:

${\sigma }_1{\sigma }_2{\sigma }_1={\sigma }_2{\sigma }_1{\sigma }_2$

${\sigma }_2{\sigma }_3{\sigma }_2={\sigma }_3{\sigma }_2{\sigma }_3$

Het kan worden aangetoond dat alle andere relaties tussen de vlechten

${\sigma }_1,{\sigma }_2$ en ${\sigma }_3$ al volgen uit deze relaties en de groepsaxioma's.

Als dit voorbeeld wordt gegeneraliseerd naar $n$ strengen, kan de groep $B_n$ op abstracte wijze worden gedefinieerd via de volgende groepspresentatie:

• voortbrengers ${\sigma }_1,\dots ,{\sigma }_{n-1}$
• relaties, bekend als de vlechtrelaties of de relaties van Artin:
  • ${\sigma }_i{\sigma }_j={\sigma }_j{\sigma }_i$ als $|i-j|\ge 2$;
  • Voor $i=1,\dots ,n-2$ is ${\sigma }_i{\sigma }_{i+1}{\sigma }_i={\sigma }_{i+1}{\sigma }_i{\sigma }_{i+1}$. Dit wordt wel de vergelijking van Yang-Baxter genoemd.

Deze definitie beschouwt met als de algebraïsche definitie van een vlechtgroep.

Eigenschappen

De groepen $B_0$ en $B_1$ zijn triviale groepen, $B_2$ is de oneindige additieve groep van de gehele getallen $\mathbb{Z}$, $B_3$ is een oneindige groep die niet commuatief is en is isomorf met de knoopgroep van de klaverbladknoop.

Alle elementen in $B_n$, die niet de identiteit zijn, hebben een oneindige orde, $B_n$ is met andere woorden torsie-vrij. Als $n>2$ is, bevat $B_n$ een vrije groep op twee generatoren, dus is geen abelse groep. Men kan dit ook inzien door vast te stellen dat $B_n$ afbeeldt op de symmetrische groep $S_n$, die niet-abels is.

$B_n$ is een ondergroep van $B_{n+1}$ en kan worden gezien als opgebouwd uit alle vlechten op de $n+1$ strengen, waarbij de onderste streng horizontaal is en geen enkele andere kruist of doorkruist wordt door een andere vlecht. De vereniging van alle vlechtgroepen wordt wel de oneindige vlechtgroep genoemd.

Verband met knopentheorie en berekenbaarheid

Als men voor een gegeven vlecht het eerste voorwerp aan de linkerkant met het eerste voorwerp aan de rechterkant verbindt, en dit voor de tweede, derde en volgende voorwerpen links en recht herhaalt, waarbij men steeds een nieuwe streng gebruikt, zonder enige vlechten in de nieuwe strengen te creëren, ontstaat een schakel en soms een knoop. De stelling van Alexander in de vlechttheorie stelt dat het omgekeerde ook waar is: iedere knoop en iedere schakel ontstaat op deze manier uit ten minste een vlecht. Deze vlecht kan worden gevonden door de schakel door te snijden. Aangezien vlechten in de generatoren ${\sigma }_i$ concreet als woorden kunnen worden gegeven, geeft men bij het invoeren van knopen in computerprogramma's vaak de voorkeur aan deze methode .

Websites

• Sjabloon:En Sjabloon:Aut en Sjabloon:Aut. Braid Groups, 2008. Sjabloon:ISBN
• MathWorld. Braid Group.