Vereniging (verzamelingenleer)

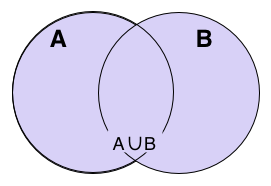
In de verzamelingenleer is de vereniging of unie van een collectie verzamelingen de verzameling die bestaat uit alle elementen van de samenstellende verzamelingen. Zo bestaat de vereniging van de verzamelingen $A$ en $B$ uit alle elementen die tot $A$, $B$ of allebei behoren.

Definitie

De vereniging $A\cup B$ van de verzamelingen $A$ en $B$ is de verzameling die bestaat uit alle elementen van $A$ en van $B$:

$A\cup B=\{x\mid x\in A\text{ of }x\in B\}$

De doorsnede en het verschil van twee verzamelingen worden op een overeenkomende manier gedefinieerd.

Voorbeeld

Zij $A=\{1,2,6,10,12\}$ en $B=\{1,2,5,8\},$ dan is $A\cup B=\{1,2,5,6,8,10,12\}.$

Eigenschappen

• De vereniging is een associatieve en commutatieve operatie, dus:

$A\cup (B\cup C)=(A\cup B)\cup C=A\cup B\cup C$

en

$A\cup B=B\cup A$

• De vereniging is distributief over de doorsnede:

$A\cup (B\cap C)=(A\cap B)\cup (A\cap B)$

en omgekeerd is de doorsnede distributief over de vereniging:

$A\cap (B\cup C)=(A\cup B)\cap (A\cup B)$

• Veronderstel dat er een verzameling $A$ is, waar twee andere verzamelingen $B$ en $C$ een deelverzameling van zijn.

$B\subseteq A$ en $C\subseteq A$

Definieer het relatieve complement van een deelverzameling van $A$ ten opzichte van $A$ als het verschil tussen $A$ en die deelverzameling, bijvoorbeeld $A\setminus B$.

Dan zijn

$B\cup C=A\setminus ((A\setminus B)\cap (A\setminus C))$ en $B\cap C=A\setminus ((A\setminus B)\cup (A\setminus C))$

Deze twee eigenschappen komen met de wetten van De Morgan overeen uit de wiskundige logica.

• $x\in \bigcup _{i\in I}{V}_i\iff \mathrm{\exists }i\in Ix\in V_i$ waarin $I$ een indexverzameling is.

• Het aantal elementen in de vereniging $\bigcup _{i=1}^n{V}_i$ van een $n$ verzamelingen $V_i$ is

$|\bigcup _{i=1}^n{V}_i|=\sum _{i=1}^n|V_i|-\sum _{i<j}^n|V_i\cap V_j|+\sum _{i<j<k}^n|V_i\cap V_j\cap V_k|-\cdots \pm (-1{)}^{n+1}|V_1\cap \cdots \cap V_n|$

Generalisatie

Zij $X$ een willekeurige verzameling en $ℱ$ een familie deelverzamelingen van $X.$ De familie $ℱ$ mag oneindig of zelfs overaftelbaar veel verschillende deelverzamelingen van $X$ bevatten.

De vereniging van $ℱ$ is de deelverzameling van $X$ die bestaat uit alle elementen $x\in X$ die tot minstens één lid van de familie $ℱ$ behoren.

In het bijzonder is de vereniging van een lege familie dus leeg.

De veronderstelling van het bestaan van de universumverzameling $X$ is nodig om paradoxen te vermijden. De vereniging van een willekeurige familie verzamelingen is binnen de axiomatische verzamelingenleer niet gedefinieerd.