Dihedrale groep

Fout bij het aanmaken van de miniatuurafbeelding:

Sneeuwvlok

In de groepentheorie en de meetkunde, deelgebieden van de wiskunde, is een dihedrale groep of diëdergroep de groep van symmetrieën van een regelmatige veelhoek. Voor $n\ge 3$ wordt de groep van symmetrieën van een regelmatige $n$-hoek genoteerd als ${\mathrm{D}}_n$ of ${\mathrm{D}\mathrm{i}\mathrm{h}}_n$. De groep heeft $2n$ elementen, namelijk $n$ draaiingen en $n$ spiegelingen. De eenvoudigste dihedrale groep is de groep $D_3$ die isomorf is met de symmetriegroep van een gelijkzijdige driehoek.

De symmetriegroep van het vierkant wordt genoteerd als ${\mathrm{D}}_4$. Een sneeuwvlok heeft de dihedrale symmetrie van een regelmatige zeshoek. De symmetriegroep ervan is ${\mathrm{D}}_6$.

De dihedrale groep wordt in het algemeen in twee dimensies als de groep van symmetrieën van een regelmatige veelhoek beschreven, maar kan ook in drie dimensies worden beschreven. De beschrijvingen zijn isomorf.

De dihedrale groep is voor $n$ vanaf drie te interpreteren als een permutatiegroep van de hoekpunten van een regelmatige veelhoek. De dihedrale groepen vormen een rij van groepen. Dat zijn de symmetriegroepen van de regelmatige veelhoeken onder draaiing en spiegeling. Ze hebben een dekpunt waardoor $n$ spiegellijnen lopen, waarvan twee opeenvolgende een hoek maken van 180°$/n$. Dat levert bij draaiing over een hoek van 360°$/n$ dezelfde figuur op. Er zijn zo regelmatige n-hoeken met symmetrie ${\mathrm{D}}_n$, dus vanaf $n=3$. Dihedrale groepen zijn eindige groepen, behoren tot de eenvoudigste voorbeelden daarvan en spelen een belangrijke rol in de groepentheorie, de meetkunde en de scheikunde. Bij gelijkstelling van symmetriegroepen van figuren die uit elkaar ontstaan door een directe isometrie, is er voor een gegeven vlak voor iedere waarde van $n$ precies een zo'n groep ${\mathrm{D}}_n$.

${\mathrm{D}\mathrm{i}\mathrm{h}}_n$ is alleen abels, dus commutatief voor $n=1$ en $n=2$. ${\mathrm{D}\mathrm{i}\mathrm{h}}_n$ komt voor deze waarden nog niet met de symmetriegroep van een regelmatige veelhoek overeen. ${\mathrm{D}\mathrm{i}\mathrm{h}}_3$ is de kleinste groep, die niet commutatief is.

De cyclische groep ${\mathrm{C}}_n$ is een ondergroep van de dihedrale groep ${\mathrm{D}}_n$. Er zijn alleen de rotaties element van ${\mathrm{C}}_n$ en die zijn dat ook van ${\mathrm{D}}_n$. De spiegelingen die in ${\mathrm{D}}_n$ voorkomen, zijn geen element van ${\mathrm{C}}_n$. De dihedrale groep ${\mathrm{D}}_n$ is weer een ondergroep van de symmetrische groep ${\mathrm{S}}_n$.

Een variant is de oneindige dihedrale groep.

Drie dimensies

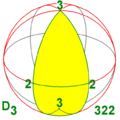
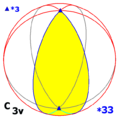
De symmetriegroep ${\mathrm{D}}_n$ in drie dimensies heeft ook hier de orde $2n$. De beschrijving van de groep gaat aan de hand van een fundamenteel domein, in dit geval een tweehoek, die 1/6 van het boloppervlak omvat. Er zijn twee beschrijvingen mogelijk. Er komen in de eerste beschrijving $n$ omwentelingsassen en een verticale rotatie-as voor, maar niet meer symmetriën. Er komen in de tweede beschrijving weer $n$ omwentelingsassen, maar nu nog een spiegelvlak voor.

Het stelsel van spiegellijnen heeft in de tweede beschrijving dus zelf rotatiesymmetrie met twee keer meer spiegelvlakken dan dat er omwentelingsassen voor de rotatiesymmetrie zijn.

De symmetriegroep van de rechthoek heet de viergroep van Klein en is isomorf met ${\mathrm{D}}_2$

• D3 in drie dimensies Sjabloon:Legenda
  ${\mathrm{D}}_3$ in drie dimensies Sjabloon:Legenda
• Bestand:Sphere symmetry group c3v.png

Voorbeeld

Onderstaande figuur illustreert de zestien elementen van de dihedrale groep ${\mathrm{D}}_8$. De bovenste rij toont de rotaties en de onderste de spiegelingen.

Bestand:Dihedral8.png