Tetratie

Sjabloon:Zie artikel Tetratie is de operatie van het herhaald machtsverheffen, waarbij het resultaat van een machtsverheffing steeds wordt gebruikt als exponent bij de volgende, terwijl het grondtal steeds gelijk blijft. Tetratie is een rekenkundige bewerking van de vierde orde en kan in termen van machtsverheffen als volgt worden gedefinieerd:

$a\uparrow \uparrow b:={}^{b}a:=a^{a^{{.}^{{.}^{{.}^a}}}}\}b=\underset{b}{\underbrace{a\uparrow a\uparrow \cdots \uparrow a}}$

waarbij de machtsverheffingen zoals gebruikelijk van rechts naar links worden uitgevoerd.

De samengestelde bewerking is hier geschreven als $b-1$ keer machtsverheffen met grondtal $a$, beginnend bij $a$, maar gelijkwaardig is het $b$ keer machtsverheffen met grondtal $a$, beginnend bij $1$ uiterst rechts:

$a\uparrow \uparrow b:={}^{b}a:=a^{a^{{.}^{{.}^{{.}^{a^1}}}}}\}b=a\underset{b}{\underbrace{\uparrow a\uparrow \cdots \uparrow a\uparrow }}1$

Vergelijk machtsverheffen, dat herhaald vermenigvuldigen is met factor $a$, beginnend bij $a$ of 1, en vermenigvuldigen, dat herhaald optellen is met term $a$, beginnend bij $a$ of 0. De belangrijkste nieuwigheid is dat de volgorde van de machtsverheffingen een rol speelt, omdat de bewerking machtsverheffing in tegenstelling tot de optelling en de vermenigvuldiging niet associatief is.

De notatie $a\uparrow \uparrow b$ is een relatief eenvoudige versie van Knuths pijlomhoognotatie met "slechts" twee pijlen, terwijl de notatie ${}^{b}a$ als Ruckers notatie bekendstaat. Bij Ruckers notatie dient er zorg voor gedragen te worden dat er geen verwarring ontstaat bij uitdrukkingen van de vorm $a^{b}c$, want behalve in speciale gevallen geldt namelijk dat $\left(a^b\right)c\ne a\left({}^{b}c\right)$.

Deze notatie wordt in andere talen ook wel de toren van machten of machtentoren genoemd.

Voorbeeld

Na som, product en machtsverheffen is tetratie de vierde bewerking die deze reeks voortzet. Met tetratie wordt een opvolging van machten benoemd, bijvoorbeeld:

${}^{4}2=2^{2^{2^2}}=2^{\left(2^{\left(2^2\right)}\right)}=2^{\left(2^4\right)}=2^{16}=65.536$

Tetreren levert voor zelfs relatief kleine waarden grote getallen op. Zo heeft ³5 reeds 2185 cijfers en ³8 bevat er meer dan 15 miljoen.

Een bijzondere tetratie

Een bijzondere functie $f:A\to ℝ$ vormt de volgende limiet van tetraties:

$f(x)=\underset{n\to \mathrm{\infty }}{\lim }{}^{n}x$

Hierin is $A$ de verzameling van reële limietpunten van $f$.

De Lambert-W functie $W(x)$ is impliciet gedefinieerd als de inverse functie van $w\mapsto w{e}^w$, zodat $v=w{e}^w\leftrightarrow w=W(v)$.

Een andere uitdrukking voor f

Bij het bepalen van de limiet in f wordt opgemerkt dat

$y=\underset{n\to \mathrm{\infty }}{\lim }{}^{n}x=\underset{n\to \mathrm{\infty }}{\lim }{}^{n+1}x=x^y$

$x=\sqrt[y]{y}=y^{\frac{1}{y}}$

$\log x=\frac{\log y}{y}$

$y\log x=-\log \frac{1}{y}$

$e^{-y\log x}=\frac{1}{y}$

$-\log x=-y\log (x)e^{-y\log x}$

$-y\log x=W(-\log x)$

$y=\frac{W(-\log x)}{-\log x}$

Hieruit volgt dat

$f:A\subset ℝ\to ℝ:x\mapsto -\frac{W(-\log x)}{\log x}$

Het domein en beeld van f

Merk allereerst op dat voor $x<0$ het niet zo hoeft te zijn dat $f(x)\in ℝ$. Uit $y=\sqrt[x]{x}$ uit de vorige sectie volgt dat het domein van f wordt beperkt door het beeld van $x\mapsto \sqrt[x]{x}$ onder $ℝ$. Zij nu

$g:[0,\mathrm{\infty }[\to ℝ:x\mapsto \sqrt[x]{x}$

een functie. We weten nu uit de vorige sectie dat g de inverse van f is. Om de karakteristieken van f te vinden is het dus voldoende om g te onderzoeken. Bepaal hiertoe eerst het maximum van het beeld van g om A vast te leggen.

$0=\frac{\mathrm{d}}{\mathrm{d}x}\sqrt[x]{x}=\frac{\mathrm{d}}{\mathrm{d}x}{e}^{\log \sqrt[x]{x}}=\frac{\mathrm{d}}{\mathrm{d}x}{e}^{\frac{\log x}{x}}=\sqrt[x]{x}(\frac{1}{x^2}-\frac{\log x}{x^2})=x^{\frac{1}{x}-2}(1-\log x)$

Merk op dat $g^{\prime }(0)$ niet gedefinieerd is, maar dat $\underset{x\to 0}{\lim }g(x)=0$ een minimum is op de rand van het domein van g. Merk verder op dat $\underset{x\to \mathrm{\infty }}{\lim }g(x)=1$ en dus dat $\underset{x\to \mathrm{\infty }}{\lim }\frac{\sqrt[x]{x}}{x^2}=0$ op grond van de productregel. De enige voorwaarden waarvoor geldt dat $\frac{\sqrt[x]{x}}{x^2}=0$ is dat $x\to 0$ of $x\to \mathrm{\infty }$, maar deze punten zitten niet in het domein van g en gelden dus niet als extreme waarden.

Dit moet betekenen dat als g een extreme waarde heeft in x, dat dan $1-\log x=0\Rightarrow x=e$. g heeft een maximum bij e.

Hieruit volgt dat $g(e)=\sqrt[e]{e}$ en dus zal het domein van f worden gegeven door $A=]0,\sqrt[e]{e}]$.

Om de waarde van f in $\sqrt[e]{e}$ te bepalen merk op dat f en g elkaars inverse zijn op het domein van f. En dus geldt $f\left(\sqrt[e]{e}\right)=e$.

De afgeleide van f

Om de afgeleide van f te bepalen gebruik de uitdrukking uit de tweede sectie:

$y=x^y$

$\frac{\mathrm{d}}{\mathrm{d}x}y=\frac{\mathrm{d}}{\mathrm{d}x}{x}^y$

$y^{\prime }=\frac{\mathrm{d}}{\mathrm{d}x}{e}^{y\log x}$

$y^{\prime }=x^y(y^{\prime }\log x+\frac{y}{x})$

$y^{\prime }(1-x^y\log x)=x^y\frac{y}{x}$

$y^{\prime }=\frac{y{x}^y}{x(1-x^y\log x)}$

$f^{\prime }(x)=\frac{f(x)\cdot x^{f(x)}}{x-x^{f(x)+1}\log x}$

Het uitwerken van deze laatste uitdrukking geeft dat

$f^{\prime }(x)=\frac{e^{-2W(-\log x)}}{x+xW(-\log x)}$

De primitieve van f

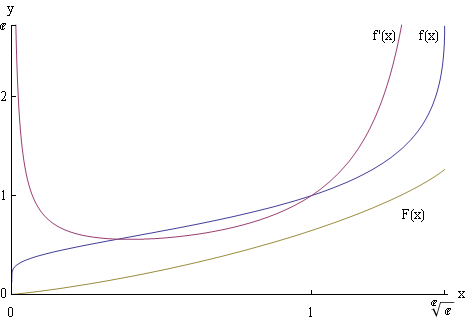
Om de primitieve van f te bepalen, zie de plot van f en g:

De oppervlakte onder f op $[0,1]$ kan impliciet berekend worden met $1-\underset{0}{\overset{1}{\int }}g(x)\mathrm{d}x$. In het algemeen geldt dat

$\mathrm{\forall }a\in ]0,\sqrt[e]{e}]:\underset{0}{\overset{a}{\int }}f(x)\mathrm{d}x=af(a)-\underset{0}{\overset{f(a)}{\int }}g(x)\mathrm{d}x$

$\mathrm{\forall }a<b\in [0,\sqrt[e]{e}]:\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x=\underset{0}{\overset{b}{\int }}f(x)\mathrm{d}x-\underset{0}{\overset{a}{\int }}f(x)\mathrm{d}x$

$=af(a)-bf(b)-\underset{0}{\overset{f(a)}{\int }}g(x)\mathrm{d}x+\underset{0}{\overset{f(b)}{\int }}g(x)\mathrm{d}x$

$=af(a)-bf(b)+\underset{f(a)}{\overset{f(b)}{\int }}g(x)\mathrm{d}x$

Hiermee verplaatsen we het probleem van integratie naar de functie g. Het blijkt dat ook g niet expliciet te integreren is, al kan wél partiële integratie toegepast worden op de volgende convergente Taylorreeks.

$\sqrt[x]{x}=e^{\frac{\log x}{x}}=\sum _{n=0}^{\mathrm{\infty }}\frac{{\log }^{n}x}{x^n\cdot n!}$

Merk op dat $\mathrm{\forall }n\in \mathbb{N}:\underset{x\downarrow 0}{\lim }\frac{{\log }^{n}x}{x}=-\mathrm{\infty }$. Dit zal ons straks problemen op gaan leveren bij de bepaling van $\underset{0}{\overset{1}{\int }}g(x)\mathrm{d}x$. Voor nu zullen we verdergaan met het bepalen van de volgende integraal

$\int \frac{{\log }^{n}x}{x^n}\mathrm{d}x=\frac{{\log }^{n}x}{(1-n)x^{n-1}}-\frac{n}{1-n}\int \frac{{\log }^{n-1}x}{x^n}\mathrm{d}x$

$\int \frac{{\log }^{0}x}{x^n}\mathrm{d}x=\int \frac{1}{x^n}\mathrm{d}x=\frac{1}{(1-n)x^{n-1}}$

$\int \frac{{\log }^{n}x}{x^n}\mathrm{d}x=\sum _{k=0}^n\frac{{\log }^{n-k}x}{(1-n)x^{n-1}}\cdot \frac{n!}{(n-k)!}\cdot \frac{1}{(1-n{)}^k}$

$=\frac{n!}{(1-n)}\sum _{k=0}^n\frac{{\log }^{n-k}x}{(1-n{)}^k\cdot x^{n-1}}$

Hieruit volgt nu dat

$\int \sqrt[x]{x}\mathrm{d}x=\int \sum _{n=0}^{\mathrm{\infty }}\frac{{\log }^{n}x}{x^n\cdot n!}\cdot \mathrm{d}x$

$=\sum _{n=0}^{\mathrm{\infty }}\int \frac{{\log }^{n}x}{x^n\cdot n!}\mathrm{d}x$

$=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\cdot \frac{n!}{(1-n)}\sum _{k=0}^n\frac{{\log }^{n-k}x}{(1-n{)}^k\cdot x^{n-1}}$

$=\sum _{n=0}^{\mathrm{\infty }}\sum _{k=0}^n\frac{{\log }^{n-k}x}{(1-n{)}^{k+1}\cdot x^{n-1}}$

Hoewel de waarde van $\underset{0}{\overset{1}{\int }}f(x)\mathrm{d}x$ niet in radicalen valt uit te schrijven is er met behulp van bovenstaande formules wél een benadering mogelijk:

$\underset{0}{\overset{1}{\int }}f(x)\mathrm{d}x=1-\underset{0}{\overset{1}{\int }}g(x)\mathrm{d}x\approx 1-0,353497=0,646503$

De visualisatie van f

Hieronder volgt een grafische visualisatie van f, $f^{\prime }$ en $F(x)=\underset{0}{\overset{x}{\int }}f(y)\mathrm{d}y$.

Zie ook

• Knuths pijlomhoognotatie
• Ruckers notatie

Externe links

• Sjabloon:En MathWorld: Pijlnotatie
• Sjabloon:En MathWorld: Power Tower