UNIQUAC-model

UNIQUAC-beschrijving (krommen) van de experimentele activiteitscoëfficiënten (datapunten) voor het binaire mengsel van (chloroform/methanol)

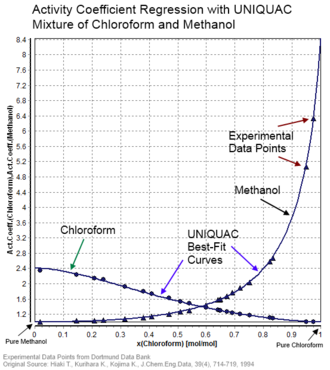
UNIQUAC (de porte-manteau voor universal quasichemical) is een activiteitscoëfficiëntmodel dat door Abrams en Prausnitz in 1975 werd ingevoerd en dat vooral in de chemische industrie wordt gebruikt voor de beschrijving van vaste stof-vloeistof-, vloeistof-vloeistof- en gas-vloeistof-fasenevenwichten. Het statistisch-thermodynamische model veronderstelt dat de lokale samenstelling rondom een molecuul niet gelijk is aan de samenstelling in de bulk, omdat op korte afstand associatie kan optreden. Dit idee is ontleend aan het model van Wilson, dat echter alle moleculen als bollen van gelijke grootte veronderstelt. De associatie wordt in het UNIQUAC-model gezien als een quasi-chemische binding. Dit idee stelde Guggenheim in 1940 ook al voor in zijn quasi-chemische theorie. Deze quasi-bindingen kunnen de zwakke vanderwaalskrachten zijn, de sterkere elektrostatische wisselwerkingen, zoals de dipool-dipoolinteractie, of de vrijwel permanente waterstofbruggen. Aanvankelijk werd het model opgesteld als een roostermodel, maar deze aanname is later niet essentieel gebleken. De interactiebeschrijving tussen moleculen wordt in het UNIQUAC-model volgens een eerste-orde-benadering afgeleid. In deze benadering wordt de lokale beschrijving rondom een type molecuul onafhankelijk gezien van dat van een ander type molecuul met zijn lokale samenstelling. Dit is in de werkelijkheid niet het geval, en daardoor is het UNIQUAC-model niet volledig consistent. Voor niet al te extreme interacties is echter het verschil tussen UNIQUAC en het consistente COSMOSPACE te verwaarlozen.

Het UNIQUAC-model kan gezien worden als een tweede generatie van activiteitscoëfficiëntmodellen, omdat de vergelijking voor de excess gibbsenergie bestaat uit een entropie- en een enthalpieterm, waarbij de entropieterm rekenschap geeft aan de grootte en vorm van de moleculen. Dit is een verbetering ten opzichte van eerdere modellen, zoals dat van Van Laar, dat van Wilson en het NRTL-model, dat alle moleculen beschouwt als bollen van dezelfde afmeting.

Vergelijkingen

Het UNIQUAC-model deelt de gibbsenergie op in een combinatoir en een residueel deel:

$G^E=(G^E{)}^C+(G^E{)}^R$

Dit is ook te zien aan de logaritmische activiteitscoëfficiënt van component i^th in het mengsels:

$\ln {\gamma }_i=\ln {\gamma }_i^C+\ln {\gamma }_i^R$

De eerste, de combinatoire term, is een entropie-term die de afwijking ten opzichte van een ideaal mengsel kwantificeert ten gevolge van de vorm en de grootte van het molecuul. De laatste is de energetische term. Hierbij wordt aangenomen dat de verandering in de interne energie gelijk is aan de verandering in de enthalpie, omdat de arbeid die verricht wordt ten gevolge van de expansie of contractie van het vloeistofvolume bij het mengen te verwaarlozen is, aangezien de volumeveranderingen veelal minder dan 1% zijn en de druk meestal onder de 10 bar ligt.

Combinatoire term

De combinatoire term berekent het niet-ideale gedrag ten gevolge van verschillen in vorm en grootte. In het UNIQUAC-model wordt daarvoor de Stavermann–Guggenheimvergelijking gebruikt. Dit model vraagt als invoer de relatieve vanderwaalsvolumes r_i en oppervlaktes q_i en het coördinatie-getal van de moleculen, $z=10$. De excess gibbsenergie van het Stavermann–Guggenheimmodel is:

$\frac{{\left(G^E\right)}^C}{RT}=\sum _i{x}_i\ln V_i+\frac{z}{2}{q}_i{x}_i\ln \frac{F_i}{V_i}$

Differentiatie van de gibbsenergie naar de molfractie van component $j$ leidt tot een uitdrukking voor de combinatoire activiteitscoefficiënt, ${\gamma }_j^C$, wat een maat is voor de partiële excess-entropie,

$\ln {\gamma }_j^C=(1-V_j+\ln V_j)-\frac{z}{2}{q}_j(1-\frac{V_j}{F_j}+\ln \frac{V_j}{F_j})$.

Hierin is de verhouding tussen de volumefractie, ${\varphi }_j$, en de molfractie van component$j$, $x_j$, gedefinieerd als $V_j$:

$V_j=\frac{{\varphi }_j}{x_j}=\frac{r_j}{\sum _k{x}_k{r}_k}$

De verhouding tussen de oppervlaktefractie, ${\theta }_j$, en de molfractie is gedefinieerd als $F_j$:

$F_i=\frac{{\theta }_j}{x_j}=\frac{q_j}{\sum _k{x}_k{q}_k}$

De combinatoire activiteitscoëfficiëntvergelijking is om te schrijven naar de som van de combinatoire term uit het model van Flory-Huggins en de correctie van Staverman-Guggenheim:

$\ln {\gamma }_j^C=(1-\frac{{\varphi }_j}{x_j}+\ln \frac{{\varphi }_j}{x_j})-\frac{z}{2}{q}_j(1-\frac{{\varphi }_j}{{\theta }_j}+\ln \frac{{\varphi }_j}{{\theta }_j})$.

In de limiet van oneindige verdunning bij een mengsel van twee componenten reduceren de bovenstaande vergelijkingen tot:

$\{\begin{array}{c}\ln {\gamma }_1^{C,\mathrm{\infty }}=1-\frac{r_1}{r_2}+\ln \frac{r_1}{r_2}-\frac{z}{2}{q}_1(1-\frac{r_1{q}_2}{r_2{q}_1}+\ln \frac{r_1{q}_2}{r_2{q}_1})\\ \ln {\gamma }_2^{C,\mathrm{\infty }}=1-\frac{r_2}{r_1}+\ln \frac{r_2}{r_1}-\frac{z}{2}{q}_2(1-\frac{r_2{q}_1}{r_1{q}_2}+\ln \frac{r_2{q}_1}{r_1{q}_2})\end{array}$

Dit stelsel van vergelijkingen toont aan dat moleculen met identieke vorm en grootte, dezelfde r en q, ook dezelfde ${\gamma }_1^{C,\mathrm{\infty }}={\gamma }_2^{C,\mathrm{\infty }}=1$ hebben.

Residuele bijdrage

De residuele enthalpie-term bevat empirisch vast te stellen interactieparameters, ${\tau }_{ij}$, tussen componenten $i$ en $j$.

$\frac{{\left(G^E\right)}^R}{RT}=-\sum _j{q}_j{x}_j\ln \left(\sum _i{\theta }_i{\tau }_{ij}\right)$

Uit deze vergelijking volgt een uitdrukking voor de logaritmische residuele activiteitscoëfficiënt van component $j$ in een mengsel:

$\ln {\gamma }_j^R=q_j(1-\ln \frac{\sum _k{q}_k{x}_k{\tau }_{kj}}{\sum _k{q}_k{x}_k}-\sum _k\frac{q_k{x}_k{\tau }_{jk}}{\sum _k{q}_k{x}_k{\tau }_{kj}})$

waarin de dimensieloze interactieparameter, $\tau$, is gedefinieerd als:

${\tau }_{kj}=e^{-\mathrm{\Delta }{u}_{kj}/RT}$

$\mathrm{\Delta }{u}_{kj}$ [J/mol] is the binaire interactieenergie-parameter. Hierin is $\mathrm{\Delta }{u}_{ij}=u_{ij}-u_{ii}$, and $\mathrm{\Delta }{u}_{ji}=u_{ji}-u_{jj}$, waarin $u_{ij}$ de interactie-energie is tussen moleculen $i$ en $j$. De interactieenergie-parameters worden gebruikelijk vastgesteld aan de hand van fasenevenwichtsmetingen. In een damp-vloeistof evenwicht geldt bij lage druk bijvoorbeeld de vergelijking:

$x_j{\gamma }_j{P}_j^{\text{sat}}=y_j{P}_{\text{sys}},$

waarin $x_j$ en $y_j$ respectievelijk de molaire fracties van component $j$ in de vloeistof- en gasfase zijn, $P_j^{\text{sat}}$ de verzadigingsdruk van pure component $j$, en $P_{\text{sys}}$ de totale druk van het damp-vloeistofsysteem bij thermodynamisch evenwicht. In het algemeen geldt dat de interactie-energie voor component $i$ in een oplossing van component $j$ anders is dan dat van component $j$ in een oplossing van component $i$: $\mathrm{\Delta }{u}_{ij}=u_{ji}-u_{ii}\ne \mathrm{\Delta }{u}_{ji}=u_{ji}-u_{jj}$. Dit wordt veroorzaakt door het verschil in verdampingsenergie: $u_{jj}\ne u_{ii}$, aangezien de paar interactie-energie zelf symmetrisch is: $u_{ij}=u_{ji}$. Als $\mathrm{\Delta }{u}_{ij}=\mathrm{\Delta }{u}_{ji}$ dan is er geen excess energie (warmte-effect) bij het mengen; noch een endothermisch noch exothermisch effect. In dat geval geldt ${\gamma }_i^R=1$.

In sommigen chemische processimulatorsoftware wordt de volgende functie gebruikt voor de grootheid ${\tau }_{ij}$:

$\ln {\tau }_{ij}=A_{ij}+B_{ij}/T+C_{ij}\ln (T)+D_{ij}T+E_{ij}/T^2$.

De coëfficiënten A, B,C, D en E worden uit evenwichtsmetingen bepaald. Het toepassingsbereik van het UNIQUAC-model neemt toe met het aantal bekende parameters. Dit is ongeveer 0-50°C bij gebruik van alleen parameter A, -25-75°C bij parameter A en B, -50 - 150°C bij parameter A, B en C. Een sterkere temperatuurafhankelijkheid, waarvoor een D en E parameter nodig zijn, doet zich voor bij de beschrijving van het fasenevenwicht van een vloeistof-vloeistof ontmenging rondom het kritische punt. De oorzaak ligt in het optreden van lokale concentratiefluctuaties, die de aanname van lokale concentratieverhoudingen niet meer geldig maakt.

Voor de situatie waarbij één molecuul van type $1$ is opgelost in een pure vloeistof van molecuul type 2 en omgekeerd, zijn de vergelijkingen voor de residuele activiteitscoëfficiënten:

$\{\begin{array}{c}\ln {\gamma }_1^{R,\mathrm{\infty }}=q_1(1-\ln {\tau }_{21}-{\tau }_{12})\\ \ln {\gamma }_2^{R,\mathrm{\infty }}=q_2(1-\ln {\tau }_{12}-{\tau }_{21})\end{array}$

Toepassingen (fasenevenwichtsberekeningen)

Activiteitscoëfficiënten kunnen worden gebruikt om eenvoudige fasenevenwichten te beschrijven en te extrapoleren naar temperatuurgebieden buiten het gemeten bereik. Hiermee kunnen multicomponentmengsels worden doorberekend, hetgeen belangrijk is in de berekeningen van massabalansen van een chemische fabriek.

Bepaling van parameters

UNIQUAC vereist twee basisparameters: het relatieve oppervlak en volume van een molecuul. Deze worden respectievelijk genoteerd als: q_i en r_i. Ze worden afgeleid uit het Vanderwaals-oppervlak en volume van een molecuul. De empirische parameters in het UNIQUAC-model zijn de binaire interactie-energieparameters. Deze parameters moeten voor elke binaire interactie in een multicomponentmengsel bekend zijn. In een multicomponentmengsel van $N$ componenten zijn er $N(N+1)/2$ binaire parametersets nodig. Omdat dit experimenteel tijdrovend is, wordt een deel van deze binaire sets voorspeld met de UNIFAC-methode.

Bij de bepaling van binaire interactieparameter bij multicomponentsystemen die vloeistof-vloeistof ontmenging vertonen, is het vaak noodzakelijk consistentie aan te tonen door naast de binaire ook de multicomponent-subsystemen mee te nemen. Deze noodzaak wordt veroorzaakt door de genomen eerste-orde-benadering voor de lokale interacties in het UNIQUAC-model.

Verdere ontwikkelingen

UNIQUAC is door verschillende onderzoeksgroepen uitgebreid voor verschillende toepassingen en verbeterd. Enkele noemenswaardige ontwikkelingen:

• UNIFAC is in de groepsbijdragemethode gebaseerd op UNIQUAC. UNIFAC deelt een molecuul op in bekende subgroepen. In bijzondere gevallen is het UNIQUAC gelijk aan het UNIFAC-model voor mengsels van stoffen, waar de moleculen als geheel worden beschouwd. Voorbeelden zijn de binaire mengsels water-methanol, methanol-acrylonitril en formaldehyde-dimethylformamide.
• Een thermodynamisch consistente vorm van UNIQUAC is COSMOSPACE en het equivalente GEQUAC-model.
• Extended-UNIQUAC is een uitbreiding naar waterige elektrolietsystemen.
• Uitbreiding naar een betere temperatuurafhankelijkheid van de activiteitscoëfficiënten

Zie ook

• Chemisch evenwicht
• Chemische thermodynamica
• Fugaciteit
• Activiteitsmodel van Margules, empirisch activiteitscoëfficiëntenmodel
• Vergelijking van Van Laar, activiteitscoëfficiëntenmodel gebaseerd op de vergelijking van Van der Waals; beschouwt moleculen als bollen
• MOSCED, empirisch voorspellend activiteitscoëfficiëntenmodel bij oneindige verdunning