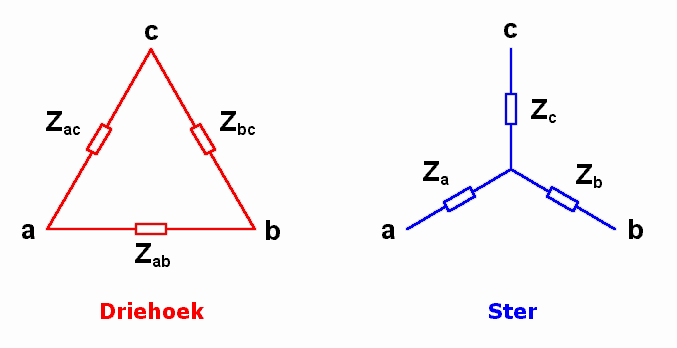
Ster-driehoektransformatie

De ster-driehoekstransformatie is een rekenmethode om van een lineair elektrisch netwerk in de vorm van een driehoek, een equivalent netwerk te bepalen in de vorm van een ster, of andersom. Deze transformatietheorie werd gepubliceerd door Arthur Edwin Kennelly in 1899.

Basis ster-driehoektransformatie

Schema in woorden: De drie knooppunten a, b en c vormen een driehoekig of een stervormig netwerk.

• De (complexe) impedanties tussen de hoekpunten van de driehoek zijn Z_ab, Z_ac en Z_bc.
• De ster bestaat uit de impedanties Z_a, Z_b en Z_c.

Omrekenformules voor driehoek naar ster

$Z_a=\frac{Z_{ab}{Z}_{ac}}{Z_{ab}+Z_{ac}+Z_{bc}}$

De volgende formules worden meestal ook genoemd, maar zijn overbodig. Ze ontstaan uit de bovenstaande door verwisseling van de hoekpunten.

$Z_b=\frac{Z_{ab}{Z}_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}$

$Z_c=\frac{Z_{ac}{Z}_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}$

Omrekenformules voor ster naar driehoek

$Z_{ab}=Z_a+Z_b+\frac{Z_a{Z}_b}{Z_c}$

Ook hier geldt dat de onderstaande formules uit de bovenstaande volgen door verwisseling van de hoekpunten.

$Z_{ac}=Z_a+Z_c+\frac{Z_a{Z}_c}{Z_b}$

$Z_{bc}=Z_b+Z_c+\frac{Z_b{Z}_c}{Z_a}$

Een meer symmetrische vorm van de omrekenformule is:

$Z_{ab}=\frac{Z_a{Z}_b+Z_a{Z}_c+Z_b{Z}_c}{Z_c}$

Analogie tussen de formules

Er is een interessante overeenkomst tussen de formules voor de impedanties Z en de admittanties Y = 1/Z.

Van driehoek naar ster voor de impedanties:

$Z_c=\frac{Z_{ac}{Z}_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}$

Van ster naar driehoek voor de admittanties:

$Y_{ab}=\frac{Y_b{Y}_a}{Y_c+Y_b+Y_a}$

En omgekeerd:

Van ster naar driehoek voor de impedanties:

$Z_{ab}=\frac{Z_a{Z}_b+Z_a{Z}_c+Z_b{Z}_c}{Z_c}$

Van driehoek naar ster voor de admittanties:

$Y_c=\frac{Y_{bc}{Y}_{ac}+Y_{bc}{Y}_{ab}+Y_{ac}{Y}_{ab}}{Y_{ab}}$

Afleiding

De formule van driehoek naar ster kan worden afgeleid door de impedanties tussen bijvoorbeeld a en b, met punt c "zwevend", aan elkaar gelijk te stellen. Dus is:

$Z_a+Z_b=\frac{1}{\frac{1}{Z_{ab}}+\frac{1}{Z_{ac}+Z_{bc}}}=\frac{Z_{ab}(Z_{ac}+Z_{bc})}{Z_{ab}+Z_{ac}+Z_{bc}}=\frac{Z_{ab}{Z}_{ac}+Z_{ab}{Z}_{bc}}{Z_{ab}+Z_{ac}+Z_{bc}}$

De formule van ster naar driehoek kan worden afgeleid door de admittanties tussen bijvoorbeeld a en b, met punten ca of cb kortgesloten, aan elkaar gelijk te stellen. Dit geeft een betrekking tussen admittanties (hierboven al gegeven) die vervolgens kan worden omgezet in een betrekking tussen impedanties.