Singulariteit (wiskunde)

In de wiskunde is een singulariteit in het algemeen een punt, waar een bepaalde relevante eigenschap van een wiskundig object niet is gedefinieerd.

De functie

$f(x)=\frac{1}{x}$

bijvoorbeeld kent op de reële getallenlijn een singulariteit in het punt $x=0$. De functie gaat daar naar $\pm \mathrm{\infty }$ en is er niet gedefinieerd.

De absolute waarde

$g(x)=|x|$

heeft ook een singulariteit in $x=0$, omdat de functie op dat punt niet kan worden gedifferentieerd.

Complexe functietheorie

De complexe functietheorie kent vier verschillende vormen van singulariteit. Veronderstel dat $U$ een open deelverzameling van het complexe vlak $ℂ$ is, dat het punt $a$ een element van $U$ is en dat de functie $f$ een holomorfe functie is die in een omgeving om $a$ is gedefinieerd, maar waar $a$ geen element van is: $U\setminus \{a\}$.

• Geïsoleerde singulariteiten: Stel dat de functie $f$ niet in het punt $a$ is gedefinieerd, hoewel de functie wel is gedefinieerd op $U\setminus \{a\}$.
  • Het punt $a$ is een ophefbare singulariteit van $f$, als er een holomorfe functie $g$ op alle $U$ kan worden gedefinieerd zodanig dat $f(z)=g(z)$ voor alle $z\in U\setminus \{a\}$. De functie $g$ is een continue vervanger van de functie $f$.
  • Het punt $a$ is een pool of niet-essentiële singulariteit van $f$, indien er een holomorfe functie $g$ en een natuurlijk getal $n$ bestaan, zodat $g$ op $U$ is gedefinieerd en dat $f(z)=g(z)/(z-a{)}^n$ voor alle $z\in U\setminus \{a\}$. De afgeleide in een niet-essentiële singulariteit kan al dan niet bestaan. Als $g(a)$ ongelijk is aan nul, zegt men dat $a$ een pool van orde $n$ is.
  • Het punt $a$ is een essentiële singulariteit van $f$, indien het noch een ophefbare singulariteit, noch een pool is. Het punt $a$ is dan en slechts dan een essentiële singulariteit als de laurentreeks oneindig veel machten van negatieve graad heeft.
• Vertakkingspunten komen in het algemeen voor bij meerwaardige functies, zoals $\sqrt{z}$ of $\log (z)$, die als ze op een zeker beperkt domein zijn gedefinieerd, binnen het domein eenduidig kunnen worden gedefinieerd.

Meetkunde

Veronderstel dat $V$ een affiene variëteit is, dat wil zeggen de oplossingsverzameling van een stelsel van veeltermvergelijkingen in $n$ variabelen. De raakruimte in een punt $P$ wordt bepaald door de veeltermen te vervangen door hun beste lineaire benadering in $P$. Elke veelterm $f$ afzonderlijk bepaalt een hypervlak door $P$, met als vergelijking $\mathrm{d}f(P)\cdot (X-P)=0$, en de raakruimte is de doorsnede van die hypervlakken.

Het punt $P$ heet singulier punt of singulariteit als minstens een van die hypervlakken niet goed is bepaald, omdat $\mathrm{d}f(P)=0$, dat wil zeggen dat alle partiële afgeleiden van de overeenkomstige veelterm nul zijn in $P$.

Voorbeeld

Grafiek van de kromme met vergelijking $x^3-y^2=0$. De singulariteit in (0,0) valt op aan de 'doornvorm'.

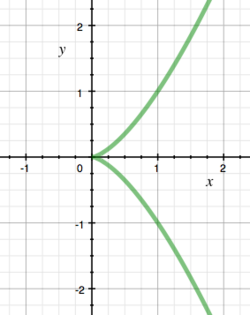
De derdegraadsveelterm in twee variabelen $x$ en $y$

$f(x,y)=x^3-y^2$

bepaalt een reële kromme in het vlak. De singuliere punten van die kromme vinden we door de partiële afgeleiden van $f$ samen gelijk te stellen aan 0:

$\frac{\partial f}{\partial x}=3x^2=0$

$\frac{\partial f}{\partial y}=-2y=0$

Hieruit volgt dat (0,0) de enige singulariteit op de kromme is.

Zelfintersectie

De kromme met vergelijking $y^2-x^2(x+1)=0$ heeft een dubbelpunt in (0,0).

Een dubbelpunt, of meer in het algemeen een punt waar de variëteit zichzelf snijdt, zodat er verscheidene raakruimtes lijken te bestaan, is altijd een singulariteit.

Een triviaal voorbeeld hiervan is de vlakke kromme die bestaat uit de vereniging van de $x$-as en de $y$-as met vergelijking $x\cdot y=0$.

Een eenvoudig niet-triviaal en irreducibel voorbeeld is de kromme bepaald door de vergelijking

$f(x,y)=y^2-x^2(x+1)$

Andere vakgebieden

• Singulariteiten komen ook in de natuurkunde voor, maar daar is een singulariteit een punt met een oneindig kleine inhoud, maar een oneindig grote massadichtheid.
• De catastrofetheorie bestudeert het lokale gedrag van functiekiemen rondom singulariteiten. Een singulariteit is in dat verband een kiem van differentieerbare functies

$f:{ℝ}^n\to ℝ$

met de eigenschap dat $f(0)=Df(0)=0$.