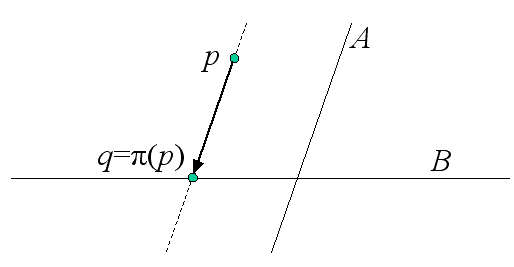Projectie (wiskunde)

Projectie in de meetkunde is een bepaald soort transformatie, waarbij een hogerdimensionale ruimte tot een lagerdimensionale ruimte terug wordt gebracht. De meetkunde kent verschillende soorten projecties of projectiemethoden.

Evenwijdige projectie

In de vlakke meetkunde definieert men de evenwijdige of parallelle projectie volgens een lijn $A$ op een andere lijn $B$, die niet evenwijdig lopen, genoteerd ${\pi }_B^A$ als de afbeelding die ieder punt $p$ op het snijpunt $q$ op $B$ afbeeldt met de unieke lijn door $p$ die evenwijdig loopt met $A$.

Dit kan in de ruimtemeetkunde worden uitgebreid voor evenwijdige projectie op een vlak volgens een gegeven richting en voor evenwijdige projectie op een lijn volgens een gegeven vlakrichting.

In het algemeen, zij $K$ een lichaam (Ned) / veld (Be) en $0\le k\le n$, dan kan men in de $n$-dimensionale vectorruimte $K^n$ een evenwijdige projectie definiëren op een $k$-dimensionale deelruimte volgens een $(n-k)$-dimensionale richting, op voorwaarde dat de gegeven deelruimte en de gegeven richting lineair onafhankelijk zijn.

Centrale projectie

In de vlakke meetkunde definieert men de centrale projectie vanuit een punt $o$ op een lijn $B$, die niet door $o$ gaat, genoteerd ${\pi }_B^o$ als de afbeelding die ieder punt $p$ op het snijpunt $q$ afbeeldt op $B$ zodat $o,p$ en $q$ op een lijn liggen. Deze functie is niet gedefinieerd voor $p=o$.

Hetzelfde kan ook in meer dimensies worden uitgevoerd.

Evenwijdige en centrale projecties zijn in de projectieve meetkunde uitingen van hetzelfde begrip, omdat richtingen geïdentificeerd worden met punten 'op oneindig'.

Overige

• Tekeningen met lijnperspectief maken van verschillende vormen van projecties gebruik.

• Er is in de lineaire algebra een manier om de loodrechte projectie van een vector op een andere vector te berekenen. Deze vectorprojectie vindt een toepassing in de gram-schmidtmethode voor het bepalen van een orthonormale basis in een vectorruimte.

• De functionaalanalyse maakt gebruik van evenwijdige projecties in oneindig-dimensionale reële of complexe vectorruimten, bijvoorbeeld banachruimten. Daarbij wordt meestal de voorwaarde gesteld dat de deelvectorruimte waarop wordt geprojecteerd, topologisch gesloten is.

• Met een cartesisch product wordt een stel projectie-afbeeldingen geassocieerd die ieder geordende paar op een vaste component van dat tupel afbeelden. Zo heeft de productverzameling $A\times B=\{(a,b)\mid a\in A,b\in B\}$ twee projecties, ${\pi }_A$ en ${\pi }_B$:
  • ${\pi }_A:A\times B\to A:(a,b)\mapsto a$
  • ${\pi }_B:A\times B\to B:(a,b)\mapsto b$

Voor een willekeurige familie verzamelingen $(A_i;i\in I)$ bestaat de productverzameling uit alle afbeeldingen $f$ van $I$ naar de vereniging $\bigcup _{i\in I}{A}_i$ zodat $f(i)\in A_i$. De $i$-de projectie is

${\pi }_i:(\prod _{j\in I}{A}_j)\to A_i:f\mapsto f(i)$

In de cartesiaanse meetkunde op ${ℝ}^2$ komt deze verzamelingtheoretische definitie neer op evenwijdige projectie met één coördinaat-as op de andere as.