Meervoudig nulpunt van een polynoom

Als het getal a een nulpunt is van de polynoom f in x, dan is f deelbaar door de factor x - a. Is f deelbaar door meerdere factoren x - a, dan heet a een meervoudig nulpunt van de polynoom. Het aantal keren k dat f deelbaar is door x - a heet de multipliciteit van het nulpunt a en a wordt een k-voudig nulpunt van f genoemd. Voor zo'n nulpunt a is er een polynoom g waarvoor geldt:

$g(a)\ne 0$

en

$f(x)=(x-a{)}^{k}g(x)$.

Een nulpunt met multipliciteit 1 wordt ook een gewoon of een enkelvoudig nulpunt genoemd. Om het aantal nulpunten van een polynoom aan te geven, kan een k-voudig nulpunt als k nulpunten worden meegeteld, nulpunten worden in dat geval naar hun multipliciteit gerekend.

Voorbeeld

Een polynoom, met een enkelvoudig nulpunt voor x = −4 en een tweevoudig nulpunt voor x = 1

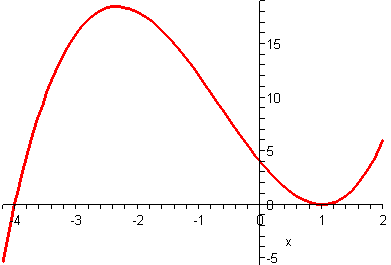
Zij gegeven het polynoom met domein $ℝ$ (zie de figuur rechts):

$f(x)=x^3+2x^2-7x+4$.

De som van de coëfficiënten $=1+2-7+4=0$, dus er geldt:

$f(1)=0$,

We kunnen nu f herschrijven als

$f(x)=(x-1)r(x)$.

Met behulp van staartdelen kan r worden bepaald:

$f(x)=(x-1)(x^2+3x-4)$.

Het polynoom $r=x^2+3x-4$ kan vervolgens worden ontbonden met de som-product-methode in $(x-1)(x+4)$, zodat:

$f(x)=(x-1{)}^2(x+4)$.

Daaruit zien we dat 1 een tweevoudig nulpunt is van het polynoom f en −4 een enkelvoudig nulpunt. Het polynoom f heeft drie nulpunten.

Hoofdstelling van de algebra

Uit de hoofdstelling van de algebra volgt, dat ieder polynoom met een graad n van ten minste 1, precies n nulpunten in het complexe vlak $ℂ$ heeft, wanneer ieder nulpunt met k als multipliciteit k keer wordt geteld.