Bézierkromme

Bézierkromme met graad drie, bepaald door vier punten

Een bézierkromme of béziercurve is in de wiskunde een type parametrische kromme, bepaald door twee of meer punten in een vlak of ruimte, die het eerste punt verbindt met het laatste, vertrekkend in de richting van het tweede punt, steeds de richting aanpassend naar een volgend punt, en aankomend bij het laatste vanuit de richting van het voorafgaande punt. De parametrische voorstelling wordt gegeven door het algoritme van Paul de Casteljau. In meer dimensies bestaan ook bézier-oppervlakken met overeenkomstige eigenschappen.

Pierre Bézier was een Franse ingenieur die deze krommen in de automobielindustrie voor Renault gebruikte.

Definitie

De béziercurve van graad $n$, bepaald door de $n+1$ punten $P_0,\dots ,P_n$ in de ${ℝ}^3$, is de parametrische kromme gegeven door:

$B(t)=\sum _{i=0}^n{b}_{i,n}(t)P_i$ met $t\in [0,1]$

Daarin zijn de $b_{i,n}$ bernsteinpolynomen gedefinieerd als:

$b_{i,n}(t)=(\genfrac{}{}{0ex}{}{n}{i})t^i(1-t{)}^{n-i}$ met $i=0,\dots ,n$

Voorbeelden

Lineaire bézierkromme

Kwadratische bézierkromme

Derdegraads bézierkromme

Vierdegraads bézierkromme

Lineaire bézierkromme

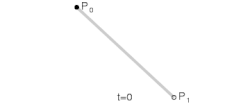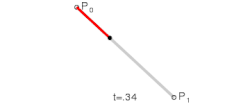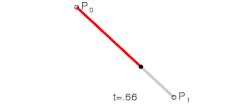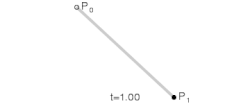
De bézierkromme van de graad een, bepaald door de twee punten $P_0$ en $P_1,$ is het verbindende lijnstuk tussen deze twee punten:

$B(t)=(1-t)P_0+t{P}_1$ met $t\in [0,1]$

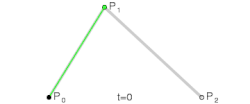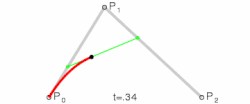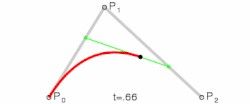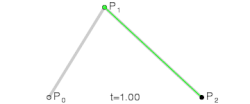
Kwadratische bézierkromme

De bézierkromme van de graad twee, bepaald door de drie punten $P_0,P_1$ en $P_2$, is de kromme:

$B(t)=(1-t{)}^2{P}_0+2t(1-t)P_1+t^2{P}_2$ met $t\in [0,1]$

De kromme ligt in het vlak door de gegeven drie punten. De drie punten uitgedrukt in coödinaten in dit vlak zijn:

$P_0=(x_0,y_0),P_1=(x_1,y_1),P_2=(x_2,y_2)$

De vergelijking van de betreffende bézierkromme is uitgeschreven

$(x-x_0{)}^2(y_0+y_2-2y_1{)}^2+$

$(y-y_0{)}^2(x_0+x_2-2x_1{)}^2-$

$2(x-x_0)(y-y_0)(y_0+y_2-2y_1)(x_0+x_2-2x_1)+$

$4[(x-x_0)(y_1-y_0)-(y-y_0)(x_1-x_0)]*$

$[(x_1-x_0)(y_0+y_2-2y_1)-(y_1-y_0)(x_0+x_2-2x_1)]$

$=0$

De kromme ligt ook in drie dimensies in het vlak door de gegeven drie punten, die zijn gegeven door $P_i=(x_i,y_i,z_i)$. De vergelijkingen voor de kromme kunnen ook daarvoor worden opgesteld, maar zijn nogal wijdlopig.

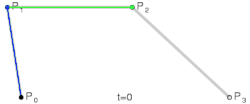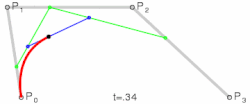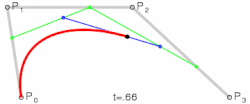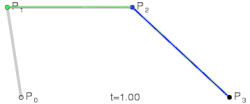
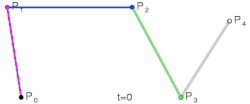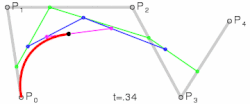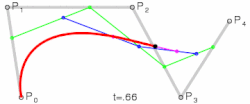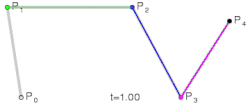
Derdegraads bézierkromme

De bézierkromme van graad drie, opgebouwd uit de vier punten $P_0,P_1,P_2$ en $P_3$, die in een vlak of in de ruimte liggen, is:

$B(t)=(1-t{)}^3{P}_0+3t(1-t{)}^2{P}_1+3t^2(1-t)P_2+t^3{P}_3$ met $t\in [0,1]$

Algemene vorm

Definieer $B_{P_0{P}_1\dots P_k}$ als de bézierkromme die door de punten $P_0,P_1,\dots ,P_k$ is bepaald. Dan zijn

$B_{P_0}(t)=P_0$ en

$B(t)=B_{P_0{P}_1\dots P_n}(t)=(1-t)B_{P_0{P}_1\dots P_{n-1}}(t)+t{B}_{P_1{P}_2\dots P_n}(t)$

Hiermee zijn de bézierskrommes op een recursieve manier gedefinieerd, die door een willekeurig aantal punten zijn bepaald.

Toepassingen

Derdegraads bézierkrommen worden veel gebruikt. Zij verbinden het beginpunt $P_0,P_1,P_2$ en eindpunt $P_3$ en kunnen door de keuze van de tussengelegen punten $P_1$ en $P_2$ zo met de gewenste begin- en eindrichting worden aangepast, zodat de kromme ook nog door een gewenst punt gaat.

Praktisch worden ze gebruikt:

• voor afbeeldingen in grafisch programma's om gladde krommen te tekenen
• in TrueType-lettertypes, die worden met eenvoudige kwadratische bézierkrommes geschreven
• voor digitale animatie om een zo natuurlijk mogelijke beweging te simuleren