Vrije-elektronenlaser

Vrije-elektronenlaser FELIX bij FOM Rijnhuizen

Een vrije-elektronenlaser is een laser die een breed scala aan golflengtes bestrijkt. Alles van microgolven tot röntgenstralen. Het grote voordeel van deze nieuwe laser, in tegenstelling tot conventionele lasers, is dat de golflengte van de laser continu instelbaar is.

Werking

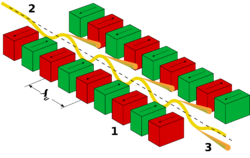
In een vrije-elektonenlaser (FEL) wordt een bundel elektronen periodiek afgebogen door een rij magneten, een undulator. De trillende elektronen genereren elektromagnetische straling, zoals een antenne. De elektronen in een FEL hebben echter een snelheid bijna gelijk aan de lichtsnelheid, waardoor de straling sterk voorwaarts gericht is.

De golflengte van de FEL straling is ($\gamma >>1$)

$\lambda =\frac{l}{2{\gamma }^2}(1+a_u^2)$.

$l$ is de undulatorperiode, $\gamma$ is de Lorentzfactor van de elektronen en $a_u$ is een maat voor de magneetveldsterkte:

$a_u\approx 0,66Bl$ met het magneetveld op de undulator-as $B$ in tesla en de undulatorperiode in cm.

De lasergolflengte kan continu gevarieerd worden door $B$ of de elektronenergie $\gamma$ te veranderen.

Afleiding

In een vereenvoudigd eendimensionaal model bestaat het veld uit het statische undulatorveld en de lasergolf met langzaam veranderende amplitude

$a_x+i{a}_y=a_u{e}^{i{k}_{u}z}+a_l(z)e^{i{\alpha }_l(z)}{e}^{-ik(z-ct)}$.

De $a$'s zijn dimensieloze vectorpotentialen, $a=eA/mc$. De $k$'s zijn golfgetallen van undulator $k_u=2\pi /l$ en laser $k=2\pi /\lambda$. De scalaire potentiaal en $a_z$ zijn 0 gesteld omdat ruimtelading verwaarloosd wordt. De benadering geldt alleen nabij de undulator-as.

De intensiteit van het veld

$a_x^2+a_y^2=a_u^2+a_l^2+2a_u{a}_l\cos (\psi -\alpha ),\psi =k_{u}z+k(z-ct)$

bevat een lopende golf, de cosinusterm, die zich voortplant met fasesnelheid $ck/(k+k_u)$. Elektronen met dezelfde snelheid wisselwerken met het veld en kunnen de lasergolf doen groeien. Deze resonantievoorwaarde is dus

${\beta }_z=k/(k+k_u)$ of $k=k_u{\beta }_z/(1-{\beta }_z)$.

Als ${\beta }_x$ en ${\beta }_y$ verwaarloosbaar zijn is $1/{\gamma }^2=1-{\beta }_z^2\approx 2(1-{\beta }_z)$ dus

$k=2{\gamma }^2{k}_u$ of $\lambda =\frac{l}{2{\gamma }^2}$.

In een sterke undulator zijn ${\beta }_x$ en ${\beta }_y$ niet verwaarloosbaar. Ze zijn te berekenen uit de veralgemeende impulsen, zie Lagrangiaan. $p_x+e{A}_x$ en $p_y+e{A}_y$ zijn constant, doordat in dit eendimensionale model geen $x$- en $y$-afhankelijkheid is. De constanten zijn 0 als de elektronen vóór de undulator alleen een $p_z$-component hebben. Dus ${\beta }_x=-a_x/\gamma ,{\beta }_y=-a_y/\gamma$.

$1/{\gamma }^2=1-{\beta }_z^2-{\beta }_x^2-{\beta }_y^2\approx 2(1-{\beta }_z)-a_u^2/{\gamma }^2$

omdat $a_l<<a_u$. Dus

$k=\frac{2{\gamma }^2{k}_u}{(1+a_u^2)}$ of $\lambda =\frac{l}{2{\gamma }^2}(1+a_u^2)$.