LC-kring

Geanimeerde werking van een LC-kring

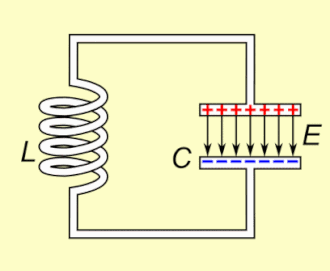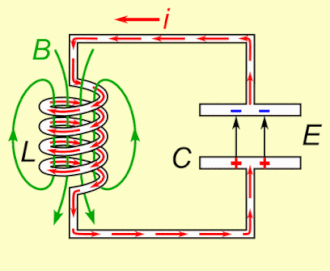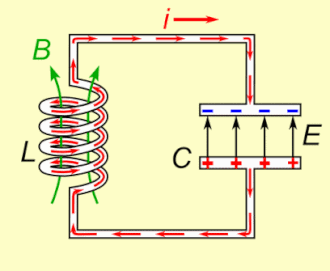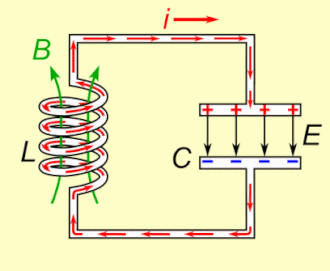
Een LC-kring is een elektrische schakeling die bestaat uit een spoel en een condensator. Er wordt, door verwaarlozing van de elektrische weerstand, verondersteld dat er geen energieverlies optreedt in het circuit.

De LC-kring gedraagt zich als een resonantiekring. Resonantiekringen vormen een belangrijk onderdeel van veel applicaties zoals oscillatoren, filters, tuners, DC-AC converters en mixerschakelingen.

Resonantiefrequentie

Een LC-kring heeft geen weerstand. Als deze kring wordt aangestoten, bijvoorbeeld door de condensator op te laden, ontstaat een oscillatie met frequentie $f_0$, waarbij periodiek energie van de condensator naar de spoel gaat en omgekeerd. Zonder weerstand treden geen verliezen op en zal de kring blijven oscilleren.

De resonantie-hoekfrequentie ${\omega }_0$ (in radialen per seconde) wordt gegeven door:

${\omega }_0=\frac{1}{\sqrt{L\cdot C}}$

waarin

$L$ de zelfinductie van de spoel in henry, en

$C$ de capaciteit van de condensator in farad

De resonantiefrequentie $f_0$ is dan:

$f_0=\frac{{\omega }_0}{2\pi }$

dus:

$f_0=\frac{1}{2\pi \sqrt{L\cdot C}}$

Berekening

Uit de spanningswet van Kirchhoff volgt dat de spanning $V_C$ over de condensator in grootte gelijk moet zijn aan de spanning $V_L$ over de spoel:

$V_C=-V_L$

Op dezelfde manier volgt uit de stroomwet van Kirchhoff dat de stromen door de condensator en de spoel aan elkaar gelijk moeten zijn:

$i_C=i_L$

Ook is

$V_L(t)=L\frac{\mathrm{d}{i}_L}{\mathrm{d}t}$

en

$i_C(t)=C\frac{\mathrm{d}{V}_C}{\mathrm{d}t}$

Na herschrijven en vervangen, volgt een tweede-ordedifferentiaalvergelijking

$\frac{{\mathrm{d}}^{2}i(t)}{\mathrm{d}{t}^2}+\frac{1}{LC}i(t)=0$

Definieer:

$\omega =\sqrt{\frac{1}{LC}}$

Met deze definitie is de differentiaalvergelijking:

$\frac{{\mathrm{d}}^{2}i(t)}{\mathrm{d}{t}^2}+{\omega }^{2}i(t)=0$

Een wellicht mogelijke oplossing invullen, van de gedaante

$i(t)=e^{at}$

levert met differentiëren en wegdelen van $e^{at}$ een voorwaarde voor $a$:

$a^2+{\omega }^2=0$,

en dus zijn er twee oplossingen voor $a$:

$a=+j\omega$

en

$a=-j\omega$

met $j$ de imaginaire eenheid.

De volledige oplossing van de differentiaalvergelijking is:

$i(t)=A{e}^{+j\omega t}+B{e}^{-j\omega t}$

De integratieconstanten $A$ en $B$ volgen uit de begincondities (de waarden van $i$ en $V$ op tijdstip nul).

Trivia

het stroomschema dat mogelijk de inspiratie vormde voor Mr. Chad

Het LC-stroomschema vormde mogelijk de inspiratie voor de creatie van Mr. Chad.

Zie ook

• RLC-kring